Description of Automatic Focus Detection Technique

Overview of the Technique

The technique used to determine whether or not an image is in focus involves the use of the power spectrum. When an image is in focus, its power spectrum returns information about the frequency-domain characteristics of the image. As the image becomes out of focus, high frequency features of the image will tend to become blurred and the cooresponding high frequency power spectrum characteristics will decrease in magnitude.

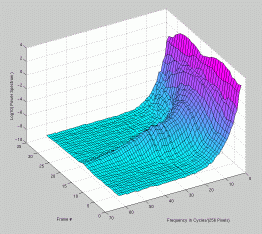
The following data sets were used to test this technique:

MVR-3041_4step (tree type??) - Set of 33 images captured at 4-step focus intervals across the focus.
MVR-3041_1step (tree type??) - Set of 21 images captured at 1-step focus intervals across the focus.
BCD-95-246_4step (tree type??) - Set of 33 images captured at 4-step focus intervals across the focus.

Computation of Power Spectrum

The power spectrum of images is approximated by the periodogram technique (see Peter D. Welch, "The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms", IEEE Transactions on Audio and Electroacoustics, June 1967). In this method, the largest power of two number of pixels and number of lines are used to compute the periodogram. For instance, if an image is 1280x1024 in size, the first 1024x1024 pixels will be analyzed. If the width to be analyzed is W and the height is H, the data will be split into nine overlapping regions of size (W/2)x(H/2), as shown in Figure 1.

Figure 1 - Overlapping Regions Used for Computing Periodogram

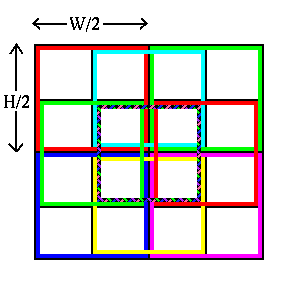
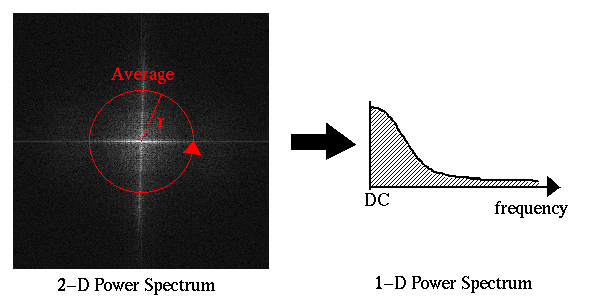
The magnitude squared of the Fourier Transform is then computed for each of the nine overlapping regions. The approximated two-dimensional power spectrum is then obtained by averaging the magnitude squared output of each of the overlapping regions. For the purposes of detecting focus, we are only interested in the magnitude of the power spectrum at high frequencies. We do not care about the orientations of various features in the power spectrum. 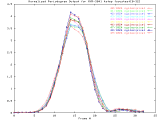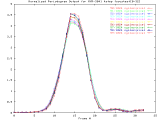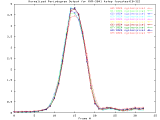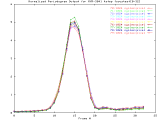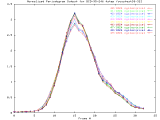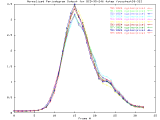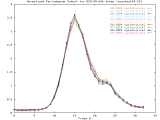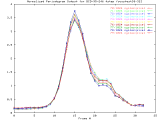For this reason, to simplify the problem the two-dimensional power spectrum can be reduced to one dimension by performing radial averaging, as shown in Figure 2.

Figure 2 - Radial Averaging of 2-D Power Spectrum

Normalization of Power Spectrum Data

In order to test the correlation between image focus and power spectrum characteristics, a series of images were captured at different focus settings. Power spectra were computed for each image for comparison. In order to normalize the power specrum from each image in order to simplify comparisons, two pre-processing steps were applied to the data:

For each image power spectrum, each frequency value is divided by the DC value for that image. This results in a curve with a value of one at the origin (DC) with high frequency values ranging from zero to one. This allows the degree of "drop-off" in intensity at each frequency step to be analyzed. The more out of focus an image is, the faster its power spectrum should "drop off" as frequency increases.
In order to study the correlation of various frequency ranges in the power spectrum to the degree of focus in the image, the output from the various test images must be further normalized to one another. To accomplish this, each frequency value is considered independently from the others. If the test set contains n images, and each image has m spectral values the n values of each spectral frequency are analyzed, one frequency at a time. For each frequency, f, the average of the n values at that frequency is computed and each of the n values are divided by this average value in order to produce a unit mean. This allows the f frequency data set to be compared to the f-1, f+1, f+2, etc., data sets.

(a) Original Power Spectrum with 1/256 and 2/256 frequency content removed and plotted as log10 of output.

(b) Normalized Power Spectrum

Figure 3 - Normalization of Power Spectrum Data

Focus Experiments

1024x1024 Image at 4 focus step intervals:

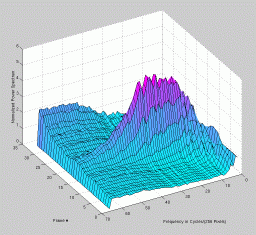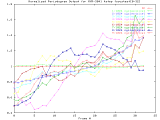
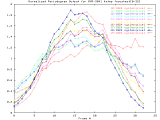
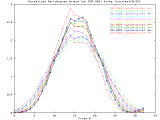
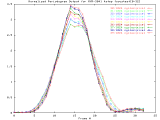
MVR-3041_4step Full Size - Set of 33 1024x1024 images taken from a typical (tree type ??) sample. The images were captured at 4 focus motor step intervals, with frame 15 at the "best" visual focus.			Sample images: frame10, frame15, frame20
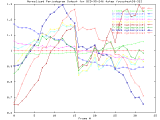
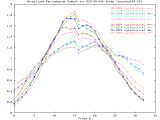
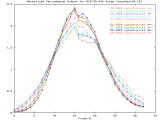
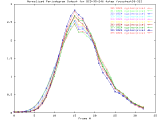
DC - 9/1024 Cycles/Pixel	10/1024 - 19/1024 Cycles/Pixel	20/1024 - 29/1024 Cycles/Pixel	30/1024 - 39/1024 Cycles/Pixel	40/1024 - 49/1024 Cycles/Pixel	50/1024 - 59/1024 Cycles/Pixel	60/1024 - 69/1024 Cycles/Pixel	70/1024 - 79/1024 Cycles/Pixel

BCD-95-246_4step Full Size - Set of 33 1024x1024 images taken from a typical (tree type ??) sample. The images were captured at 4 focus motor step intervals, with frame 15 at the "best" visual focus.			Sample images: frame10, frame15, frame20
DC - 9/1024 Cycles/Pixel	10/1024 - 19/1024 Cycles/Pixel	20/1024 - 29/1024 Cycles/Pixel	30/1024 - 39/1024 Cycles/Pixel	40/1024 - 49/1024 Cycles/Pixel	50/1024 - 59/1024 Cycles/Pixel	60/1024 - 69/1024 Cycles/Pixel	70/1024 - 79/1024 Cycles/Pixel

256x256 Image at 4 focus step intervals:

MVR-3041_4step Windowed - Set of 33 256x256 images taken from a typical (tree type ??) sample. The images were captured at 4 focus motor step intervals, with frame 15 at the "best" visual focus.			Sample images: frame10, frame15, frame20
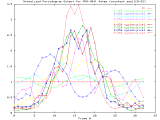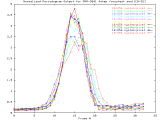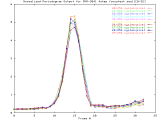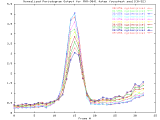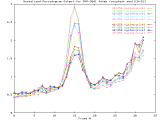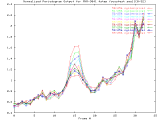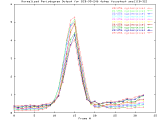
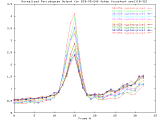
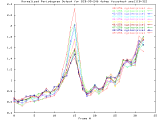
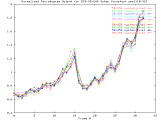
DC - 9/256 Cycles/Pixel	10/256 - 19/256 Cycles/Pixel	20/256 - 29/256 Cycles/Pixel	30/256 - 39/256 Cycles/Pixel	40/256 - 49/256 Cycles/Pixel	50/256 - 59/256 Cycles/Pixel

BCD-95-246_4step Windowed - Set of 33 256x256 images taken from a typical (tree type ??) sample. The images were captured at 4 focus motor step intervals, with frame 15 at the "best" visual focus.			Sample images: frame10, frame15, frame20
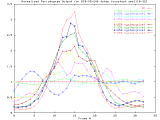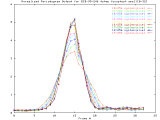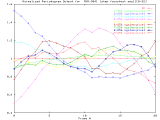
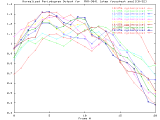
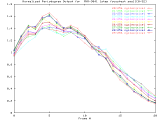
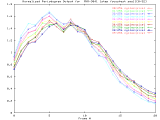
DC - 9/256 Cycles/Pixel	10/256 - 19/256 Cycles/Pixel	20/256 - 29/256 Cycles/Pixel	30/256 - 39/256 Cycles/Pixel	40/256 - 49/256 Cycles/Pixel	50/256 - 59/256 Cycles/Pixel

256x256 Image at 1 focus step intervals:

MVR-3041_1step Windowed - Set of 20 256x256 images taken from a typical (tree type ??) sample. The images were captured at 1 focus motor step intervals, with frame 5 at the "best" visual focus.			Sample images: frame0, frame5, frame20
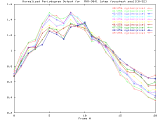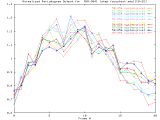DC - 9/256 Cycles/Pixel	10/256 - 19/256 Cycles/Pixel	20/256 - 29/256 Cycles/Pixel	30/256 - 39/256 Cycles/Pixel	40/256 - 49/256 Cycles/Pixel	50/256 - 59/256 Cycles/Pixel

Description of Automatic Focus Detection Technique

Overview of the Technique

Computation of Power Spectrum

Normalization of Power Spectrum Data

Focus Experiments

1024x1024 Image at 4 focus step intervals:

MVR-3041_4step Full Size -

BCD-95-246_4step Full Size -

256x256 Image at 4 focus step intervals:

MVR-3041_4step Windowed -

BCD-95-246_4step Windowed -

256x256 Image at 1 focus step intervals:

MVR-3041_1step Windowed -